Spiralen

Als je kijkt naar de Boom van Pythogoras valt onmiddellijk de spiraalstructuur op. Dergelijke spiralen vind je vaak terug in fractals, zoals in (de uiteinden van) de Kromme van Lévy.

Bij veel spiralen tref je oneindige herhaling aan. Dat, samen met het bovenstaande, doet vermoeden dat spiralen iets met fractals van doen hebben.

In het volgende laten we vier bekende spiralen de revue passeren:

1. De Afwikkelkromme of Evolvente.
2. De Concentrische spiraal of Spiraal van Archimedes.
3. De Logarithmische spiraal of Groeispiraal.
4. De Loxodroom of Bolspiraal.

De Evolvente

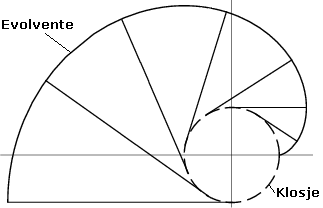
Als je een klosje garen afwikkelt en daarbij de draad strak houdt beschrijft het uiteinde van de draad een spiraal (Het klosje staat stil, je draait om het klosje heen). Deze spiraal staat bekend onder de naam Evolvente of 'afwikkelkromme'.

Deze spiraalvorm wordt onder andere toegepast in tandwiel-overbrengingen, zoals je die aantreft in de versnellingsbak van een auto. De contact-vlakken van de vertanding hebben de vorm van een evolvente.

In het fractal-gebeuren speelt de evolvente geen rol.
Opvallend is dat de spiraal een begin lijkt te hebben, maar dat is niet zo. Als je de diameter van het klosje oneindig klein maakt, blijkt dat de spiraal geen begin heeft. Daardoor is deze spiraal een fractal. De herhaling is oneindig.
De aangroei (dit is de toename van de diameter van de spiraal na één volledige omwenteling) is gelijk aan de omtrek van het klosje: πD. Deze is constant.

Deze spiraal speelt bij fractals geen rol van betekenis.

De Spiraal van Archimedes

De Spiraal van Archimes tref je overal aan waar dingen worden opgerold: een meetlint, een rol behang of vloerbedekking, enzovoort.
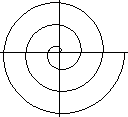Kenmerkend is dat de spiraal geen einde heeft, maar wel een duidelijk aanwijsbaar begin. Daardoor is deze spiraal geen fractal.
De aangroei is gelijk aan de dikte van wat is opgerold. Deze is constant.

Dat deze spiraal een begin heeft volgt direct uit de formule voor de voerstraal: r = aφ.
De poolhoek φ (in radialen) begint bij 0 en wordt steeds groter. Als φ = 0 is r = 0. Dit is het beginpunt van de spiraal.

Ook deze spiraal speelt in het fractal-gebeuren geen rol van betekenis.

De Groeispiraal

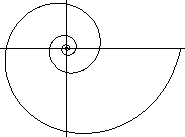
De Groeispiraal verschilt van de Spiraal van Archimedes doordat de aangroeiing per omwenteling steeds toeneemt. Dat blijkt ook uit de formule die de Groeispiraal beschrijft:

r = c e^{a φ}

Hierin is r de voerstraal en φ de poolhoek. a en c zijn constanten. Merk op dat:

• voor a > 0 neemt de straal per omwenteling toe.
• voor a < 0 neemt de straal per omwenteling af.
• voor a = 0 is de straal per omwenteling constant. Het is dus een cirkel.

Het bijzondere van deze spiraal is dat deze er op elke schaal hetzelfde uitziet. Een schaalverandering komt neer op het verdraaien van de spiraal.

De Groeispiraal is bij Fractals van groot belang. Als je in een afbeelding van een fractal een spiraal tegenkomt is dat (vrijwel) altijd een Groeispiraal.

De Bolspiraal

Een bolspiraal of loxodroom ontstaat als je met een constante snelheid over het oppervlak van een bol gaat, van de Noordpool naar de Zuidpool, terwijl de bol zelf ook met constante snelheid ronddraait.

Een bolspiraal heeft een aanwijsbaar begin- eindpunt en is dus geen fractal.
Hieronder staat een bolspiraal, getekend in twee aanzichten.

De bolspiraal staat er bij voor de volledigheid. Bij fractals spelen ze geen enkele rol.

Laatst bijgewerkt: 5 december 2013